Modeling the Price Reaction to the Implementation of a Land Value Tax: A discussion of parameter selection, assumptions, and sensitivity
July 2024 | By Jack Jol
Figure 1
The plot above illustrates the value (blue) and revenue collected (red) of land subject to a 30-year linearly increasing land value tax implementation maxing out at 75% annual land rent collection. This calculation requires a number of assumptions that will be discussed below.
First it is important to go over how we are calculating the value of land for each year. Present land value is determined according to the following rules:
To calculate the “current price” in response to the implementation of the tax, assume a buyer at year X knows only the following information:
Current value (at year X) based on previous value (at year X-1)
Percentage expected to change in value according to tax the rollout scheme for the remainder of the rollout years
Land’s Cap Rate
Years Expected to Own
And does not take risks accounting for:
Future inflation
The induced effects of the tax
These inflationary effects do interact with the land value and are observed by the following buyer as effects on the previously assessed price. Inflationary effects essentially occur between price calculations.
A buyer, with this information, calculates the sum of net rents expected to be collected throughout ownership based on the post-inflation value from the previous year.
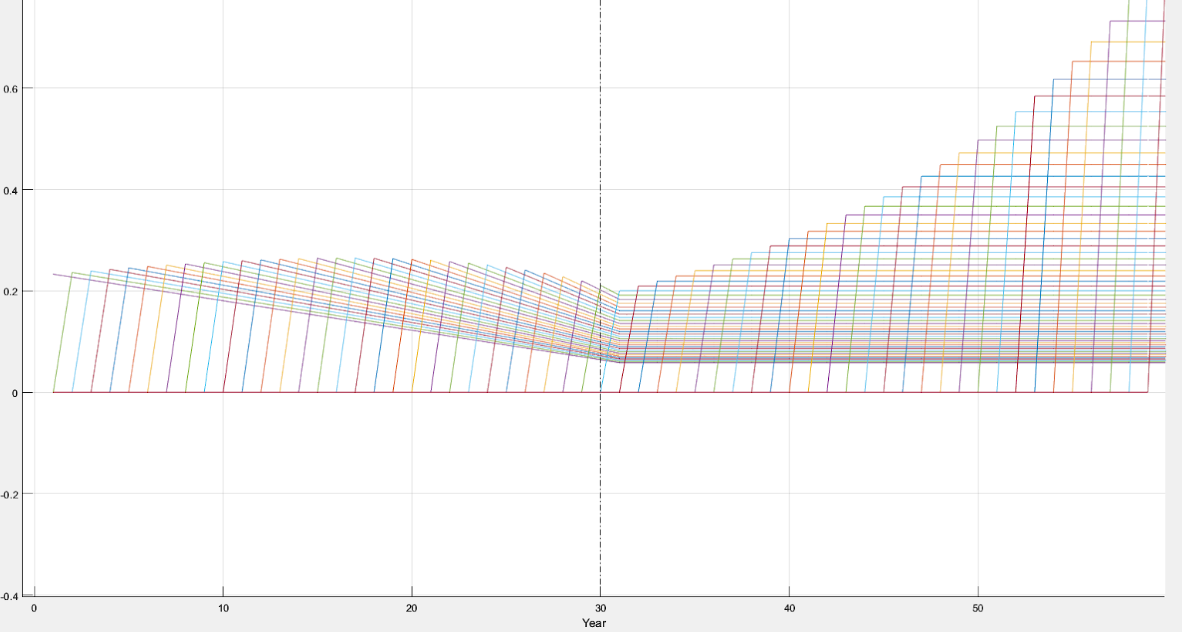
Here is a visualization of the yearly rent calculations the buyer conducts. Each line represents the series of future net rents collected for a buyer starting each year.
Figure 2
Figure 1’s value line (blue) is a series of each line in Figure 2’s sum, which is equivalent to the expected revenue over the expected course of ownership starting at any given year.
Revenue is calculated as the taxed portion of the current price. Following will be a discussion of the parameters involved in these calculations.
Parameters
Start Price
This variable, as the name suggests, is simply the initial value of the land in question. All figures in this paper have been generated with a start price of 6.4 to represent the assessed $6.4 trillion of Canadian land. Altering this value scales the model as expected.
Captured Value
The capture value is the percentage of land rental value desired to be captured by a fully implemented land tax.
Figure 3
In Figure 3, you can observe the difference the capture value makes as it is iterated from 0% to 100%. A 0% collection generates no revenue (top line), and the price inflates naturally with the inflation rate described below. At 100% collection (bottom red line) , we observe that the value of land decreases and remains at 0 over the course of the rollout. These extremes behave as expected. Other figures in this paper display the effects of a 75% capture value. This was chosen as our default for the reasons discussed in our research paper Natural Common Wealth and Economic Rent in Canada.
Rollout Time
In this model, all rollouts are linear for the sake of simplicity. For a 30 year rollout aiming for a 30% capture value would increase by 1% annually. Essentially, the rollout time marks the year where, after equal increases in the tax, the tax achieves its full specified capture value.
Figure 4
By iterating over rollout durations between 0 and 40 years in 5-year increments, we can observe the trading benefits of different rollout lengths. In orange on top, one can observe a 40-year rollout. This rollout is sufficiently slow such that the increasing tax value and effects of inflation work to stabilize the price about its starting value, holding it there for the mid-20 years of the rollout. This also results in the lowest post-rollout values, reflecting the slow-to-show induced effects we expect to see in response to a significant price drop, which will be discussed later in the paper. To contrast, a 0-year rollout (bottom blue line) shows an immediate loss of 75% of value (an undesirable occurrence for real land and housing) but offers the benefit of having the greatest and earliest exposure to induced inflationary effects and thus has the greatest post rollout values. When choosing a real rollout period for a tax such as this one, factors such as social impact, feasibility, and market impact need to be considered.
Cap Rate and Duration of Ownership
These two variables are able to be adjusted separately, but it makes sense in this model to link these parameters with a relationship of 1/CapRate = years of ownership. The cap rate is the rate of return on the property, and our “buyer” expects to hold the property with its cap rate for the exact number of years required to justify the calculated price. This is a simplification, as cap rates do fluctuate, but modeling such behavior is outside of our scope.
Figure 5
The impact of different assumed cap rates can be observed in the chart above. Ranging between a 2% (lowest blue line) and a 6% (highest orange line) cap rate by 0.5% intervals with associated ownership durations for pricing highlights the importance of a good cap rate estimate with this model. Since the “current price” at any time is calculated based on the expected returns over the ownership period, low cap rates with long ownerships see an earlier decrease in price in response to knowledge of the described tax rollout.
It is suggested that the average cap rate of land in Canada exists in the 4-6% range, following this assumption, calculations in this paper use a 4.5% cap rate. For calculations that solely look at housing, we believe the average cap rate will be lower, with data suggesting an approximate value of 2.6%. Real cap rates are subject to change over time, reflecting market activity, and as this behavior is not predictable it is not accounted for in the model.
Elasticity
This model incorporates a small elastic parameter into its calculations in hopes of better reflecting real responses in the housing market. With a change in price, we expect to see a shift in supply and demand dynamics, reflecting itself in pricing. With large price decreases, we expect to see an increase in demand, dampening the expected price change. Similarly with an increase in price, a decrease in demand, therefore dampening the price jump. Housing and land are traditionally considered inelastic or of low elasticity, so this effect is rather small.
Figure 6
In Figure 6, we can observe the effect of varying the coefficient of elasticity between 0 and 1 by increments of a tenth. This range of values was chosen because housing is considered relatively inelastic. It is clear that the impact of the elastic coefficient is very small. especially when compared to the other variables in this model. Upon closer inspection we can observe that varying the coefficient produces variance throughout the series, but is not expected to significantly alter the model’s trajectory. This can be seen with a closer inspection of the trend line as in Figure 7.
Figure 7
Incorporating Induced Growth
When constructing this model we considered the incorporation of a small induced growth effect which would occur some time after the start of the rollout. With the price to own lowered by our tax, we expect to see a boost in demand. To reflect this we included a normally distributed increase in growth rate some time after the rollout begins. We predict such an effect to be relatively small (<1%).
Figure 8
Figure 8 displays the impact of varying the peak magnitude of this induced effect between 0.1% and 1%. Such an effect is not negligible but is also not predictable(within the scope of this paper) therefore it has been left out of other calculations. To properly incorporate this induced growth we would need a better understanding of how it relates to the other variables in our model.
Additional Assumptions
This model works with the assumption that the value of land will continue to grow according to a baseline growth rate. The figures in this paper were generated with an assumed average baseline growth of 4% annually. This was selected to reflect a middle ground between urban and rural growth rates. This is a simplification, as real world growth rates vary but modeling this behavior is outside the scope of this paper.